Universa’s Mark Spitznagel published a series of posts in early 2020 to explain the role of tail hedging and convexity in a portfolio. I enjoyed the series, yet it opens more questions than it answers. That’s reasonable — it’s more of a marketing white paper than a piece of research and should be read with that understanding.
I took some notes on it and gave it the Moontower treatment — I cleaned them up for public use while inserting some of my own musings alongside notable observations.
Some opening remarks
First of all, what is Universa?
From Universa’s website:
Universa Investments L.P. (“Universa”) is an investment management firm that has specialized in risk mitigation since it was established in 2007 by Founder and Chief Investment Officer Mark Spitznagel. Spitznagel and Universa’s Distinguished Scientific Advisor, Nassim Nicholas Taleb, together began tail hedging formally for client portfolios over twenty years ago.
Universa both formalized and institutionalized the idea of tail risk hedging in 2007, providing live tail risk mitigation for clients during (and since) the 2008 crisis. Cultivated by decades of cumulative development and implementation, Universa’s risk mitigation strategies focus on maximizing convexity—the degree of portfolio loss protection provided for a given capital allocation.
My take:
Universa and Spitznagel have made their name as a “tail fund”. A tail fund can be thought of like an insurance policy. You make a small allocation as a percent of your total investable assets. If a giant risk-off event happens the fund should return a multiple of the investment. With car or life insurance, you pay a known fixed premium. A triggering event will often pay multiples of the premium.
An insurance company can provide such a service because it charges you more in premiums than the expected value of the payoff. Insurance companies price the premium by looking at actuarial data across a huge sample of the population. Smokers or folks who show poor health on a physical can expect to pay more for life insurance. The insurance company then relies on diversification across insured populations (age, geography, health profile, etc) to make reasonable assumptions about how many claims they can expect to pay out in any period.
The difference between insurance and insuring against market losses is pricing the premium. Stock markets are not governed by the laws of physics or medicine. They are competitive games where investors learn and adapt. If you buy fire insurance, you do not affect the actuarial odds of a fire burning down your house. If you sell stocks, you do affect the real world in a tiny way (yes there is a buyer for every seller, but the relative urgencies and motivations of the counterparties mean the price impact is not symmetrical). Now multiply this over many investors, and if everyone wants to buy insurance or sell stocks all at once, then it affects the odds of a large risk-off event as well as the cost of insurance.
In short, tail hedging is more art than actuarial science. That means how you define, time, structure and execute tail hedges leaves lots of room for disappointment or good luck in your actual results. This is in stark contrast to contractual insurance where the premiums and payoffs are well-defined in a table before you ever agree to terms.
I am not advocating for any specific implementation of tail-hedging or tail-hedging at all. The merit of any approach is highly dependent on a user’s goals and how well the expression of the hedge adheres to the mandate. Since by definition you are hedging rare scenarios, past performance is poor guide because sample sizes are small and markets are always changing. This means benchmarking the future performance of any tail hedge will also be difficult.
Some investment philosophy before proceeding:
We are left to reason through the merit of tail hedging with a mix of qualitative logic and observations whose persistence will always remain in question. For those of you who find this to be an unsatisfying form of nihilism, I’ll remind you that almost all investing beliefs are subject to the same constraints and yet we plow ahead with the knowledge that not all illusions are equally fragile. Our ignorance is certain but not equally distributed across the shape of a problem.
[An obvious example would be the difference between “US markets go up in the long run” and “US markets will always be higher in 20 years”. The difference between these statements focuses on important realizations — 1) your life is but a single draw from many historical lives and 2) lost decades like Japan’s stock market are possible and your assumptions often rest on mentally available US-centric survivorship biases.]
Instead, we should try to rely on approaches where the violations of assumptions are likely to do the least harm. In short, what approaches are robust to our own ignorance? We know the worst crisis is always ahead of us, but we don’t know its timing. Is your approach to wealth robust to that fact? If you do not consider the role of your human capital and personal growth as part of your portfolio, then the answer is “no” and you fail to understand what investing is at its core.
Diversify because you do not get paid for idiosyncratic risks.
Beyond that you want insurance against systemic risk. (interventions that move the density from the small drawdown to the fast one when scaled for time [the COVID selloff of 25% was very fast so it was many ex-ante standard devs...what did 1 month teeny puts look like])
Cost of insurance is likely not an issue expectations do not vary as much as realized. It's ok that the insurance has a negative return. (when a price is out on a tail it doesn't matter)
Take the small dose. Rejoice in its robustness.
Pay up for the hedge and be sure it's actually convex
A breakdown of the series
Start: Why Do People Still Invest In Hedge Funds? (5 min read)
The series opens with a short post posing (and justifying) a provocative question:
Why do people still invest in hedge funds?
I’ll take the liberty of summarizing it with my own analogy: hedge funds are to whole-life insurance while tail hedging is to term-life insurance.
Even when hedge funds did well during periods of steep systemic losses, it wasn’t enough
to make much of an overall difference unless they made up a very large percentage allocation in a portfolio. But such a large allocation would mean their underperformance the rest of the time really hurt.
The Volatility Tax (3 min read)
If you are already well versed in the difference between compounded or geometric returns vs arithmetic returns you can skip this one. I’ve also written about it in The Volatility Drain.
If not, Spitznagel’s explanation is nice and compact. He starts:
In the words of Benjamin Graham:
“The essence of investment management is the management of risks, not the management of returns. Well-managed portfolios start with this precept.”
This is the same basic message as my favorite cliché that “defense wins
championships.” (I have annoyed my hockey-player son to no end with that
one.) Indeed, we have built an entire investment business around this
principle. One doesn’t prioritize risk management over long-term compound
returns; the two priorities are very much one-in-the-same.
Minimizing this negative compounding, or paying less volatility tax, results in higher sustained CAGRs and is the very name of the game in successful investing. It is the key to the kingdom, and explains in a nutshell Warren Buffett’s cardinal rule, “Don’t lose money.” ...large drawdowns, not the average returns, are what tend to dominate long-term portfolio value.
Part 1: Not All Risk Mitigation Is Created Equally (8 min read)
This chapter highlights:
- The value of hard optionality vs reliance on negative [potentially spurious] correlations of cross-asset hedges
- Paying less volatility tax, which results in higher sustained CAGRs, is the name of the game in risk mitigation—and successful investing.
- The impact of adding convex hedge
- Uses 3 safe haven hedges examples: 90% SPX + 10% alpha 90% SPX + 10% cash 97% SPX + 3% convex insurance product
Part 2: Not All Risk Is Created Equally (9 min read)
Points to the idea that insurance and alpha style hedges can be sized conditional on how expensive the market is (ie a valuation timing signal). Work is not shown.
- With 95% statistical significance, the higher the valuations in the stock market, the greater has been the risk (or rather the certainty) of steep market losses to come. When valuations are high (as they are today, with the CAPE measuring above 30), subsequent crashes cease to be “black swans”.
- The hypothetical insurance portfolio was optimal no matter our information, and no matter our ability (or perceived ability) to predict a crash or not. It was thus the most universal and robust risk mitigation solution.
Part 3: The Wonderful Ten-Baggers (10 min read)
This chapter addresses an important question: how sensitive is the performance of a tail risk hedge to its cost?
Effective risk mitigation needs to be able to add value within a broad spectrum of very general and logical parameters. Observing how well our safe haven prototypes, particularly the insurance prototype, have held up under these requirements has led us once again, in a highly transparent fashion, to the ways that risk mitigation can go right and how it can go wrong, and the margin of error between the two.
How sensitive are our results to that assumption of a 0% arithmetic return? What happens to these results if we move that around? Specifically, we can just look at the impact across a range of insurance crash payoffs (or,equivalently, a range of stand-alone insurance payoff arithmetic average returns) on the total portfolio geometric returns, or more specifically the compound annual growth rate (CAGR) outperformance of the 97% SPX + 3% insurance portfolio over the SPX alone.
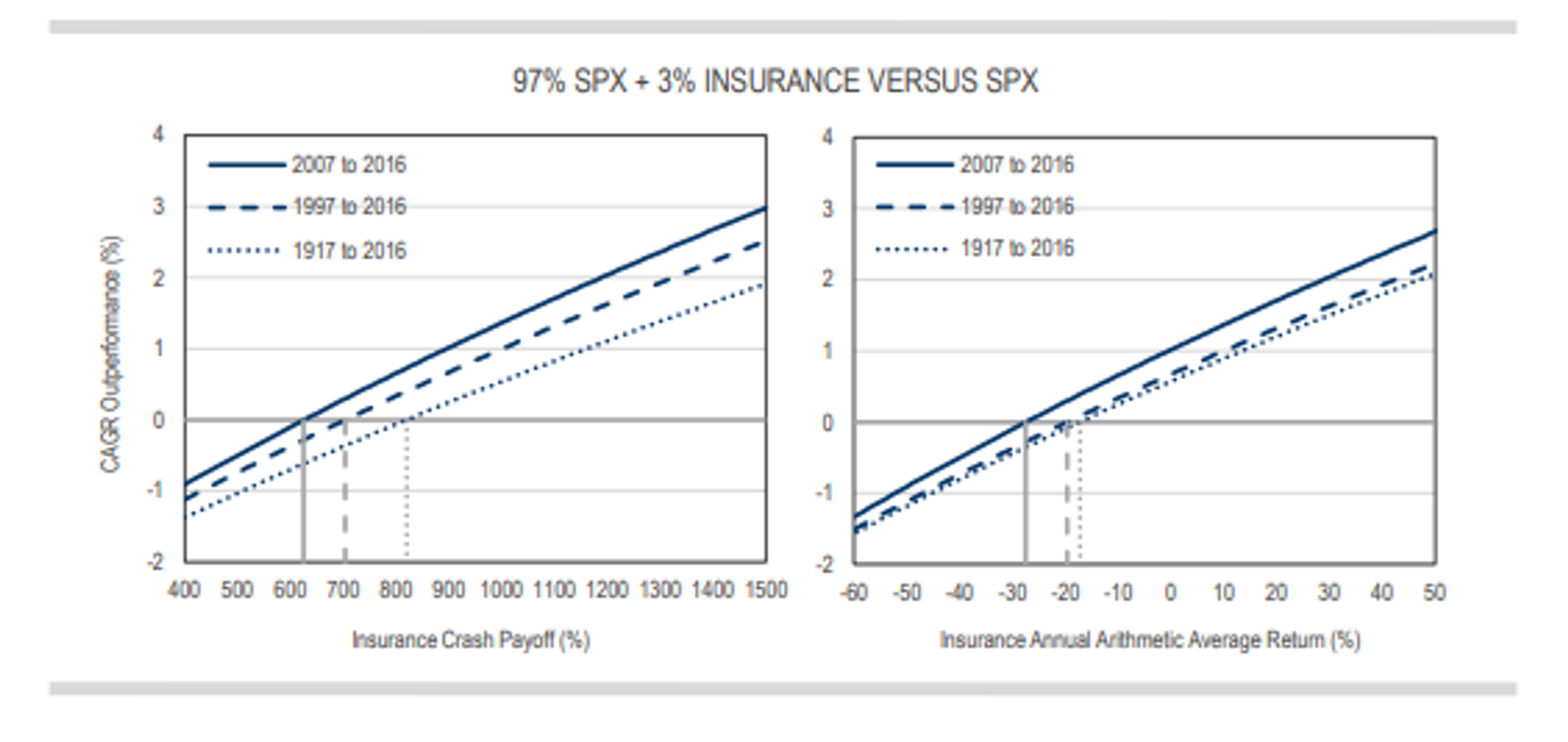
The degree of convexity that was needed to add value as a risk mitigation strategy over any specific time period depended mostly on the frequency of the systemic losses (or the “fatness of the left tail” of the SPX return distribution) during that period. The more frequent the losses, the greater the accumulated negative compounding effect, the greater the volatility tax charged to the portfolio’s CAGR, but also the more frequent the insurance crash return profits—so the less crash payoff was needed to mitigate that volatility tax.
The insurance payoff required a minimum of about an eightbagger crash payoff (an “8-to-1 longshot”) in order for it to add risk mitigation value to the portfolio through all of the three timeframes measured (with the 100-year timeframe requiring the highest payoff). This corresponded to an annual arithmetic average return for the stand-alone insurance payoff of about -20% (versus 0% for the tenbagger). At the other extreme, only about a sixbagger was required over the past 10 years, which corresponded to an annual arithmetic average return for the payoff of about -30%.
(similar result when compared to 60/40)
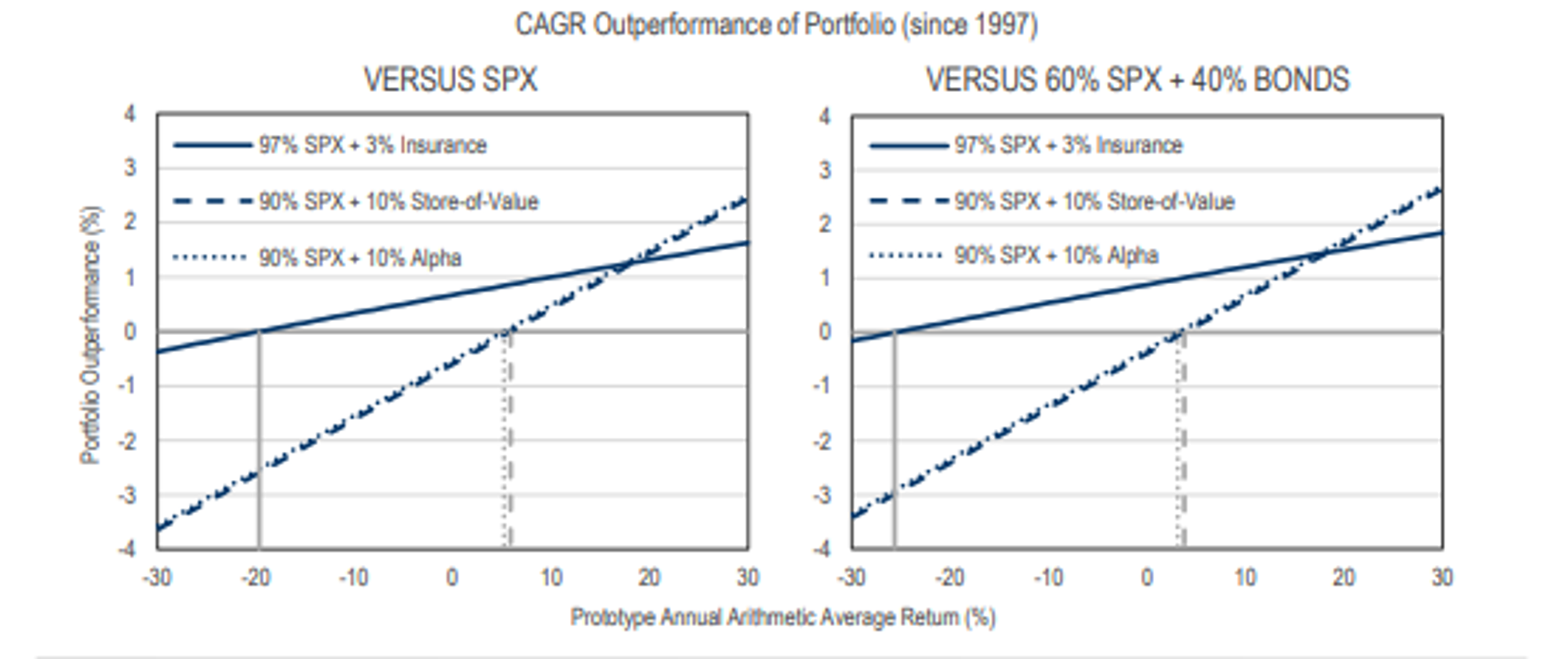
The more frequent the 15%+ drawdown, the more you can "overpay" in terms of neg EV in arithmetic return space (a more negative arithmetic return corresponds to higher insurance costs when the payouts are not a sufficiently large multiple of the premiums.)
Important takeaway: alpha prototypes have been almost the same in terms of
the risk mitigation value that they have provided to an SPX portfolio across their ranges of stand-alone arithmetic average returns
Sizing the insurance
A wonderful consequence of the wonderful tenbagger, or the extreme degree of convexity of the insurance payoff, is the very small allocation size required of that payoff in
order to move the risk mitigation needle. The fine-tuning of this sizing, both of the insurance prototype as well as of the other two prototypes, is the other important parameter
that we want to understand in terms of the sensitivity of our results.
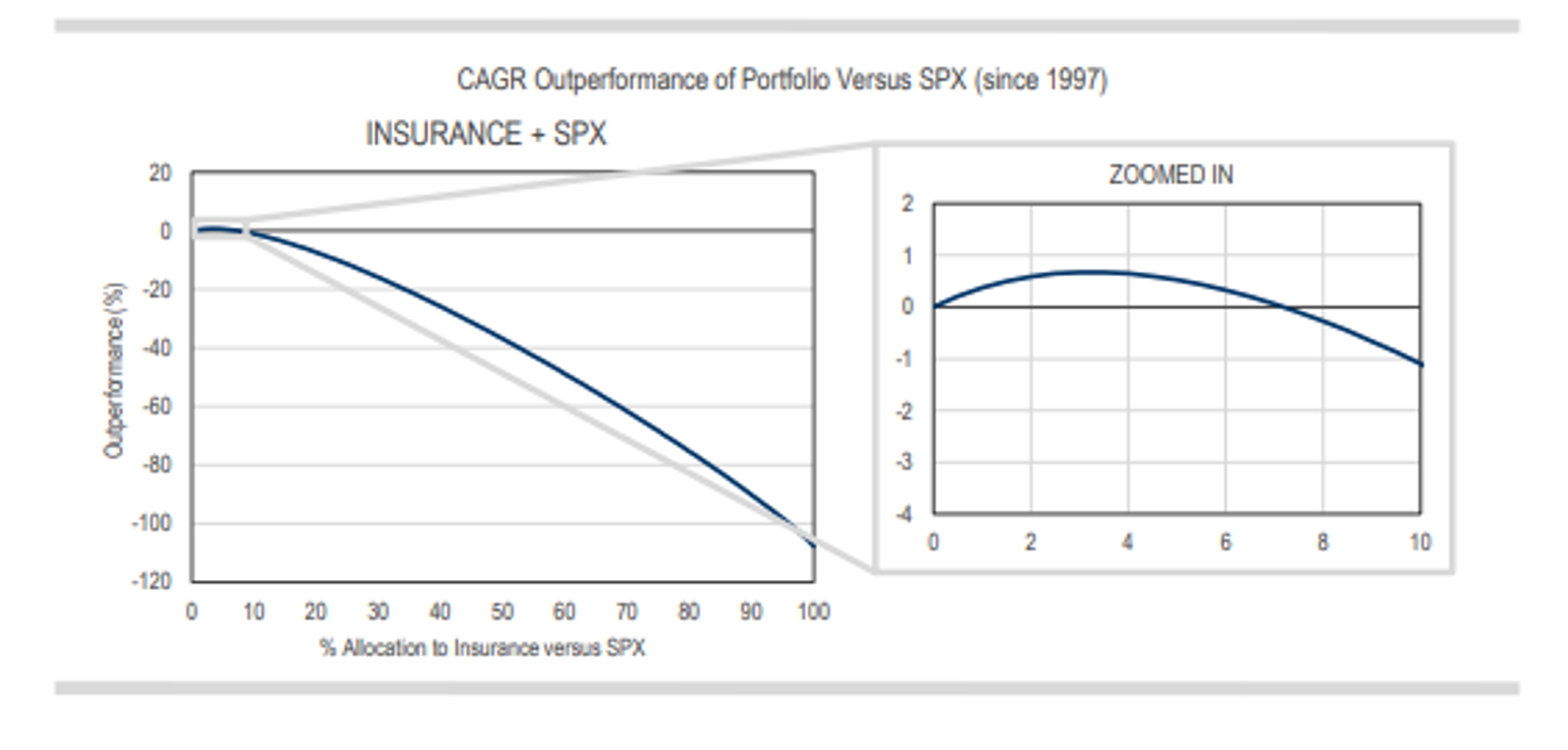
Allocations approaching 10% or higher hurt the portfolio:
In the words of the 16th century Swiss physician Paracelsus: “The right dose differentiates
a poison from a remedy.” This necessarily small 3% optimal dose of the insurance payoff—thanks to its very large “crash-bang”-for-the-buck—is such an important part
of what makes it consistently add value to a portfolio whose risk it is mitigating. Up the dose too much, and it starts to subtract value.
How we would have arrived at 3% with napkin math anyway
Conditional on the SPX being down over 15%—as we have defined the crash bucket for the safe haven prototypes—the SPX was down on average about 30% across the three time periods we looked at, and we probably would have guessed at a range of around -20% to -40% without even looking at the data. With a roughly 1000% return for the insurance prototype in that crash bucket, we would then have assumed that the required allocation to clip that tail would be about 3%. (A 1000% return on a 3% allocation equals an incremental 30% return to the portfolio, thus cancelling the loss.) So we could have arrived at our 3% allocation rather logically and, as Figure 5 makes clear, whether it was 2% or 4% (corresponding to our -20% to -40% loss guesstimate) wouldn’t have changed the results materially. The point here is there was no precise ex-post fit on the insurance allocation size in order to get the CAGR effect that we wanted. A napkin calculation would have done the same.
Robustness
The portfolio’s small required allocation for risk mitigation leaves more capital to focus on non-crash returns, in this case the SPX. This is tough for most people to appreciate, as our mental accounting tends to prefer that each portfolio line item accomplish all tasks on its own (and we have a hard time dealing with a negative number). But we can see that such clear segmentation, when done right, clearly leads to more effective risk mitigation, and consequently higher portfolio compound returns. This contrasts quite sharply with the other two safe haven prototypes, or specifically the alpha prototype which maxed out at a 35% allocation and whose impact on mitigating the negative compounding was such that moving to that optimal allocation level raised the portfolio CAGR only slightly.
Honest and effective risk mitigation needs to be robust to the realization of that risk. In fact, robustness just might be the most important attribute of effective risk mitigation. One cannot rely on a black box that worked in the past based on precise, empirically dialed-in parameters, such as sizing or timing. Effective risk mitigation needs to be able to add value within a broad spectrum of very general and logical parameters. Observing how well our safe haven prototypes, particularly the insurance prototype, have held up under these requirements has led us once again, in a highly transparent fashion, to the ways that risk mitigation can go right and how it can go wrong, and the margin of error between the two.