Here’s a stylized example:
- It’s December 1st, 2023 and a straddle expires on Friday, December 29th, the last day of the year.
- Assume your 365-day off-the-shelf model shows a 20% implied vol for the entire month. In other words, the price of the straddle over the course of the month decays exactly at its Black-Scholes prescribed theta and always imputes 20%.
Do you believe that the market’s consensus for implied volatility is actually unchanged?
I would argue that the implied vol is actually changing.
Let’s look at the measurements to start:
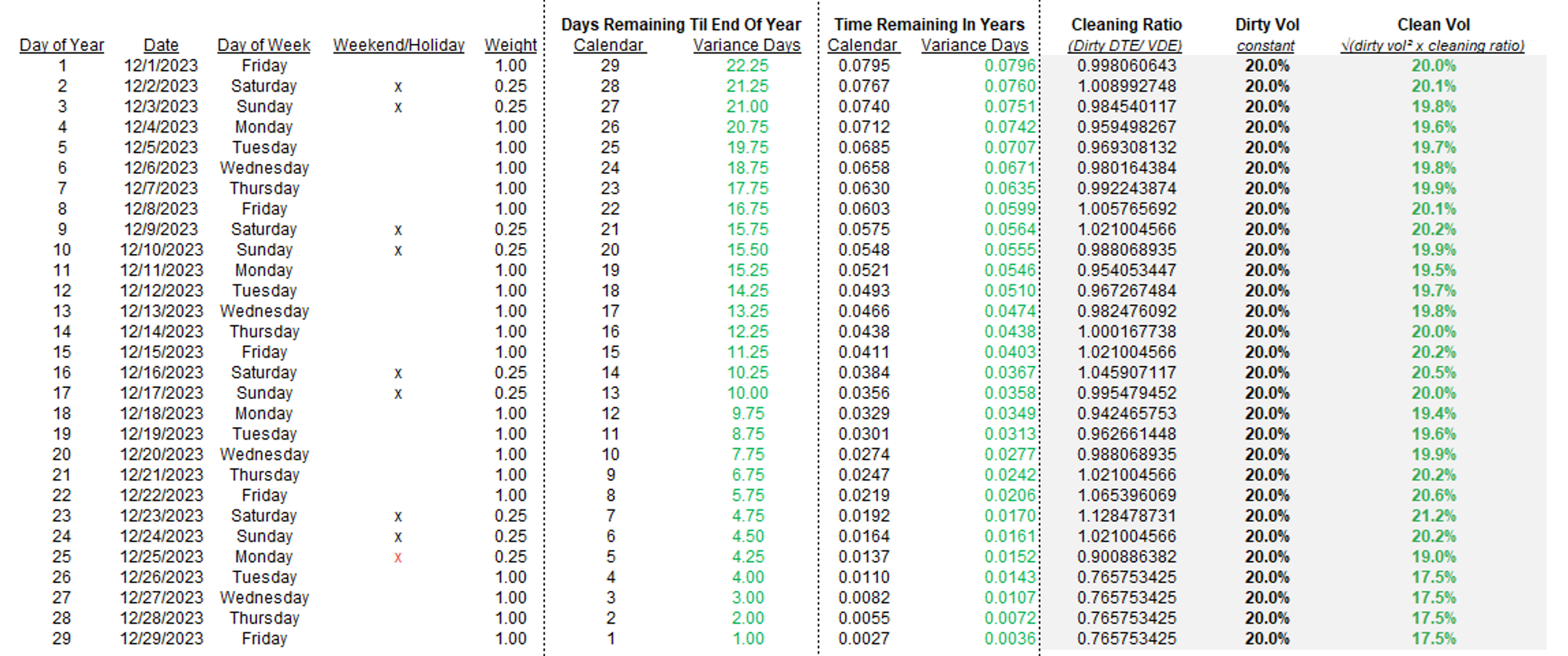
You can see the clean vol is moving around because the cleaning ratio is changing. The relative proportion of days til expiry is not static as each calendar day rolls off because the clean model assigns different weights to business and non-business days.
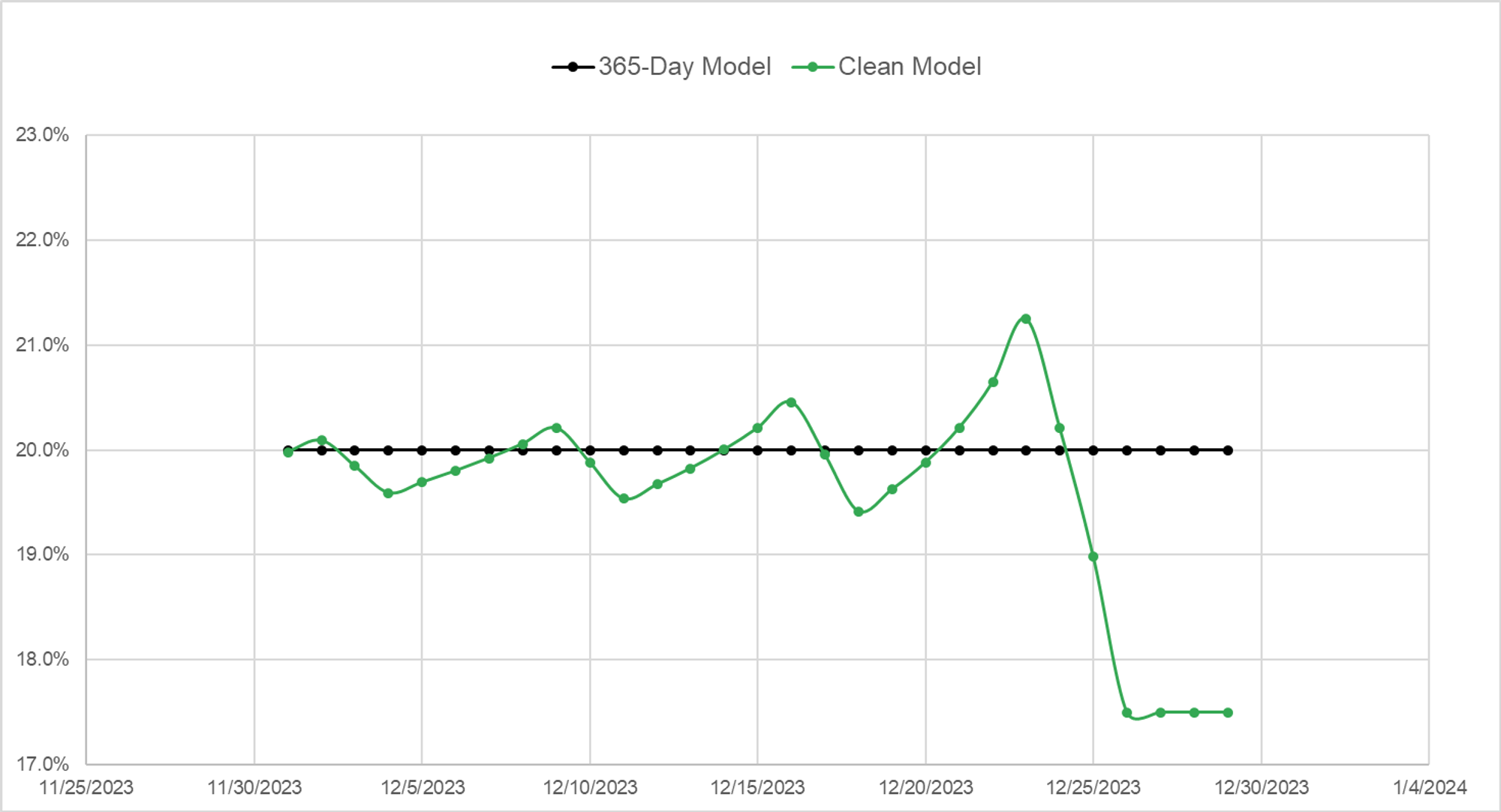
The 365-day model shows constant vol but we can see the sawtooth pattern in the clean vol.
Why?
Because as you approach a weekend (ie a business day peels off) the proportion of a year remaining in the clean model is falling faster than the calendar day model. The “variance days” are shrinking as weekends and holidays become an increasing proportion of the days remaining. Since the variance must be conserved as the time shrinks, the clean vol must be increasing.
Observationally, if you run a calendar day model it is likely you have seen the implied vol fall in your model as you approach the weekend and then rise again on Monday. Many people conflate this with some kind of calendar effect but it’s just an artifact of a naive model that ascribes the same variance to each day. If you computed clean vols this would be obvious.
To show that, let’s fix the clean vol at 20% and see what the expected changes in the dirty vol that you will observe in your off-the-shelf model will do if the clean vol is constant.
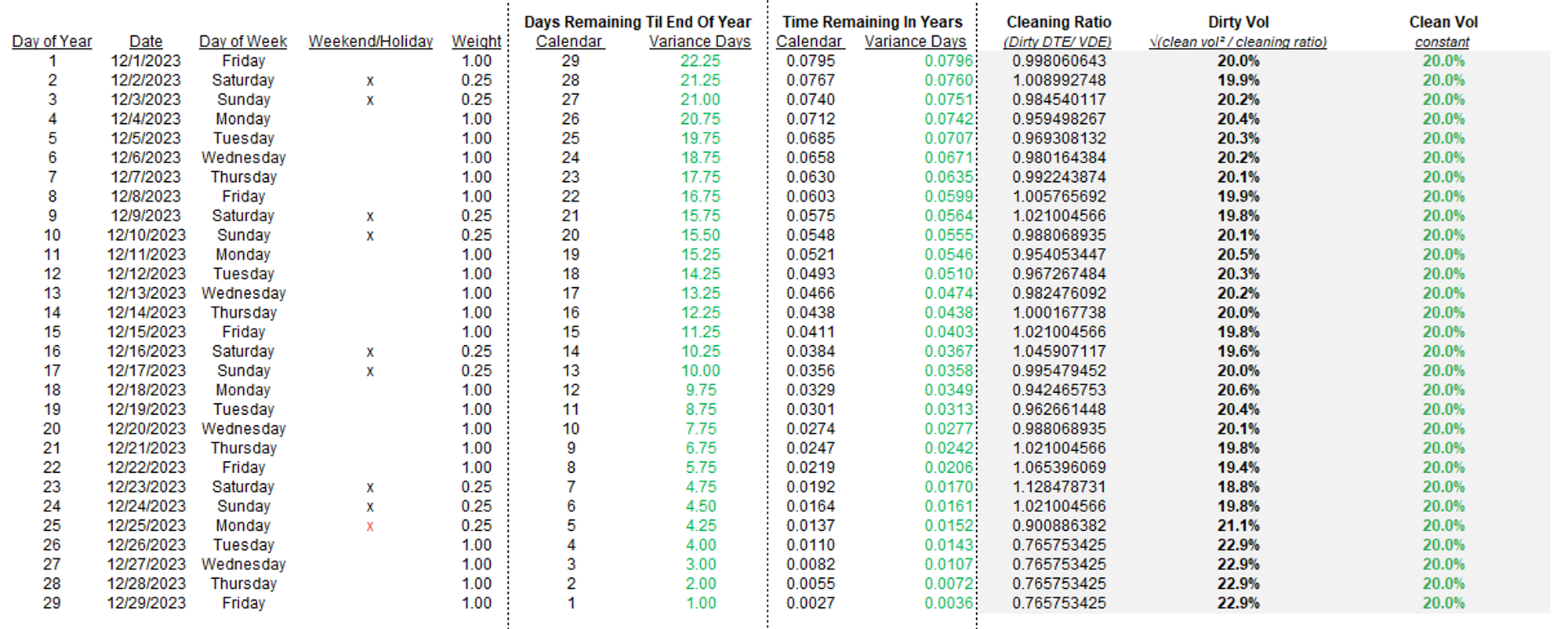
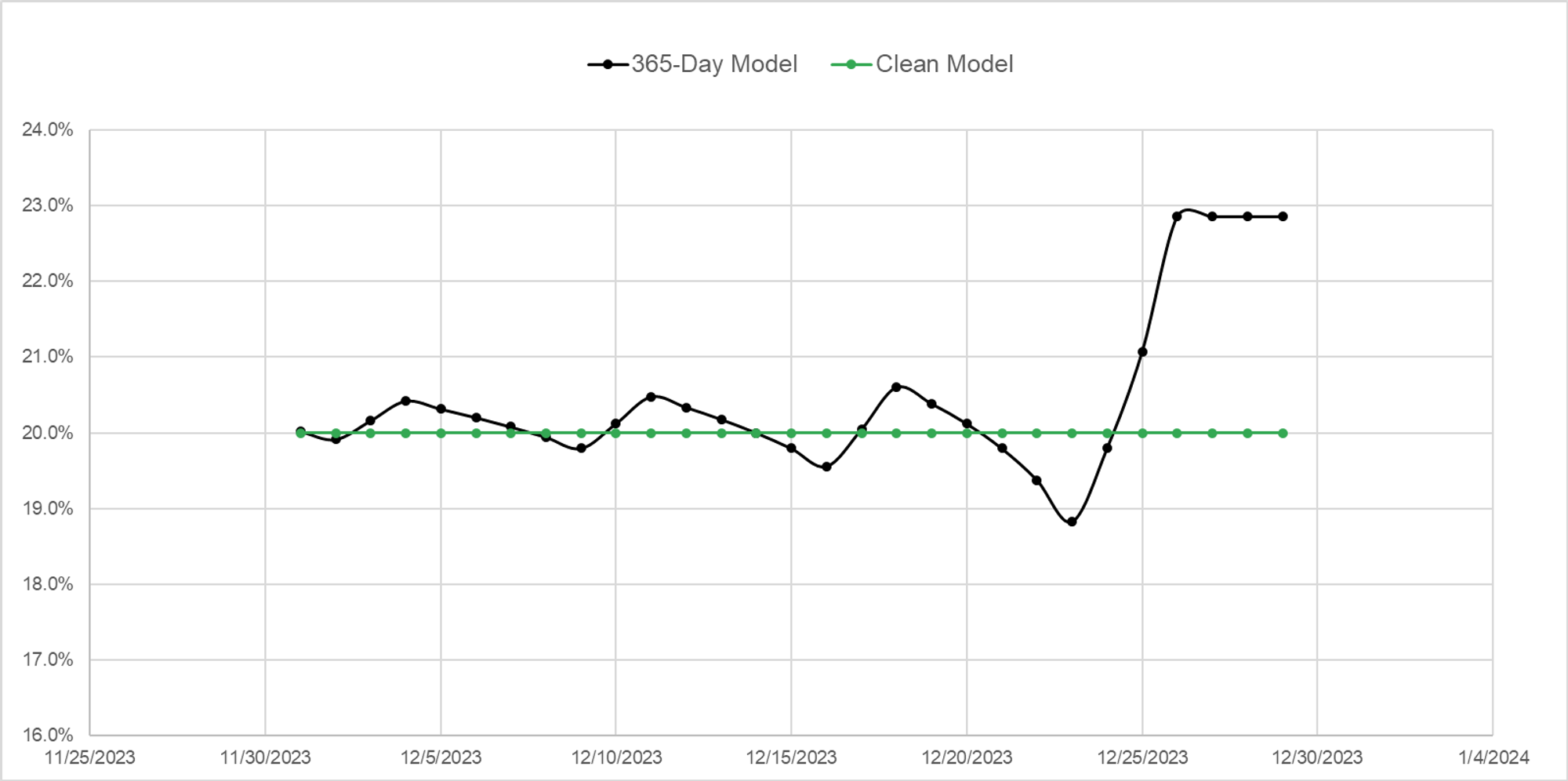
For the clean vol to actually remain fixed you will witness the implied vol in your Black Scholes model fall as we approach the weekend and then rip higher on Monday.
Think of it this way:
If the dirty IV did not fall heading into the weekend, yet you expect the weekend to have less variance than a typical business day, you’d be happy to sell the dirty IV unchanged from Monday to Friday and buy it back on Monday since the realized vol over the weekend would be less than assumption that its uniformly distributed.
Instead, the dirty IV falls during the week, and shoots back up on Monday to keep the clean or what many might consider the true implied vol the same.
If you measured IVs in clean space by normalizing by variance rather than clock time remaining you would not be tricked into thinking that IV, the market’s consensus of volatility, was changing as much as it appears to a naked eye looking at a 365-day calendar model.
Variance time passes faster during the week, but if the naive calendar model thinks all days are the same, then the dirty vol must fall because the market is smart enough to decay the straddle faster on weekdays than the weekend.
- The final section will close with a few words and mention areas for further learning.