Kelly Criterion Resources

History

Articles

Theory-focused

• The Kelly Criterion by Nicky Yoder

• The Kelly criterion: How to size bets (interactive) by Paul Butler

• Understanding the Kelly Capital Growth Investment Strategy by Prof William T Ziemba

Application-focused

• The Kelly Criterion by thezvi.wordpress.com

• The Kelly Criterion and the Importance of Money Management by Mauboussin
Notes
• “suppose the gambler’s wife allowed him to bet one dollar each week but not to reinvest his winnings. He should then maximize his expectation (expected value of capital) on each bet.” 13 In other words, if you employ the first strategy, you should focus on average payout calculated with the arithmetic mean. In this case, the mean/variance approach is the way to go. In contrast, the Kelly Criterion assumes you parlay your bets, and says you should choose the opportunities with the highest geometric means."
• Geometric return is the product of N returns to the Nth root minus 1
• Substantial empirical evidence shows that stock price changes do not fall along a normal distribution. 15 Actual distributions contain many more small change observations and many more large moves than the simple distribution predicts. These tails play a meaningful role in shaping total returns for assets, and can be a cause of substantial financial pain for investors who do not anticipate them. As a result, mean and variance insufficiently express the distribution and mean/variance can at best crudely approximate market results. Notwithstanding this, practitioners assess risk and reward using a majority of analytical tools based on faulty mean/variance metrics. So the mean/variance approach has two major strikes against it. First, it doesn’t work for parlayed bets (even though most investors do reinvest). Second, it doesn’t consider the verity of nonnormal distributions. Yet most mainstream economists still argue that maximizing geometric returns is the wrong way to allocate capital. Why?
• Neoclassical Economic Objections to the Kelly Criterion One of the most vocal critics of geometric mean maximization happens to be one of the most well-known and well-regarded economists in the world: MIT’s Paul Samuelson. Poundstone notes that Samuelson likes to describe the Kelly Criterion as a fallacy.
How do economists reconcile the apparently conflicting ideas that maximizing geometric mean will almost certainly result in higher wealth (theorem) with the notion that this approach is possibly inferior to other strategies (corollary)? Perhaps the clearest explanation of the mainstream economics case comes from Mark Rubinstein.
1. First, he notes the geometric mean maximization strategy does not assure that you will end up with more wealth than other strategies. Since the approach is based on probability, there remains a very small chance an investor will do poorly. This low-probability, high-impact scenario may violate an individual’s utility function.
2. Second, success of geometric mean maximization depends on investors staying in the market for the long run. If an investor needs access to the funds in the near-term, the benefits of compounding do not apply.
3. Third, the system assumes the investment payoffs remain steady and the investment opportunities set is large enough to accommodate a rising asset base. Shifting investment payoffs undermine the system.
4. Finally, Rubinstein invokes the macro-consistency test: to judge a strategy’s superiority, ask what would happen if everyone tried to follow it. His point is all investors cannot apply the geometric mean strategy successfully.
• One way to understand the difference of opinion is to distinguish between normative and positive arguments. Normative arguments stem from a view of how the world should be, while positive arguments reflect how things are and will likely be in the foreseeable future. Economists dismiss the strategy of maximizing geometric means based on a normative argument. Investors should have specific utility functions and act consistently with those functions. Since the small chance of a large loss will violate an individual’s utility function, geometric mean maximization is not right for everyone (Rubinstein’s first point). A positive argument is based on how people actually behave. Very few people take the time to quantify their utility functions, and those functions shift over time and with varying circumstances. In his famous Portfolio Selection, Markowitz advocates the geometric mean maximization approach. In spite of arguments by Jan Mossin (one of the founders of the capital asset pricing model) and Samuelson in the 1960s, Markowitz reconfirmed his endorsement of the geometric mean maximization strategy in the preface to his second edition published in 1970. Markowitz suggests utility-maximizing man “acts absurdly” over the long term.
• Why Many Money Managers Focus on Arithmetic Returns As we noted, geometric mean maximization requires an investor to be in the market over the long haul. If capital is free to come and go, however, as is the case with an open-end mutual fund, the portfolio manager may not have the luxury of thinking long-term. Even if geometric mean maximization is the best way to go, market realities may compel a short-term focus. The reasoning is straightforward: an open-end portfolio with poor short-run performance faces the very real prospect of losing assets. In turn, portfolio managers have a strong incentive to focus on the investment ideas they perceive will do well in the short term, even at the expense of ideas offering higher rates of return over the long term. Geometric mean maximization simply does not make sense for a portfolio manager in this short-term mindset.
• Poundstone highlights another important feature of the Kelly system: the returns are more volatile than other systems. [Kris: Poundstone is arguing for partial Kelly] While the Kelly system offers the highest probability of the most wealth after a long time, the path to the terminal wealth resembles a roller coaster. Another important lesson from prospect theory—and a departure from standard utility theory—is individuals are loss averse. Investors checking their portfolios frequently, especially volatile portfolios, are likely to suffer from myopic loss aversion. 24 The key point is that a Kelly system, which requires a long-term perspective to be effective, is inherently very difficult for investors to deal with psychologically. It is possible to reduce the strategy’s volatility by taking partial Kelly positions.
Conclusions:
• Mean/variance is not the best way to think about maximizing long-term wealth if you are reinvesting your investment proceeds. If you face a one-time financial decision, you want to maximize your arithmetic mean. But with repeated favorable opportunities—either through time or diversification—chances are you will do better in the long term by maximizing geometric mean. Mean/variance may be deeply embedded in the investment industry’s lexicon, but it doesn’t do as good a job at building wealth as a Kelly-type system.
• Applying the Kelly Criterion is hard psychologically. Assuming you do have an investment edge and a long-term horizon, applying the Kelly system is still hard because of loss aversion. Most investors face institutional and psychological constraints in applying a Kelly-type system.

• Woody Was Right by Drew Dickson (Albert Bridge Capital)

• Position Sizing Utilizing the Kelly Growth Criterion, January 2013, Market Folly

• Understanding Kelly for Portfolio management, Cameron Hight, August 2010, Alpha Theory

• St. Petersburg Paradox (How To Not Pull An FTX) by Taylor Pearson

• The Five Investor Camps that Try To Beat the Stock Market by Prof William T Ziemba

• What Gamblers Can Teach the Buy-and-Hold Crowd by Victor Haghani
• with my highlights

• Kelly’s Criterion, Founders, Startups and Bet size by Prof Jawaad Farid

Twitter Threads

• Kelly Criterion by @10kdiver

• Kelly Criterion by @FabiusMercurious

Videos

• Capital Allocation and Risk Management (Kelly) by Dr. Ernest Chan (100 min)

Extras

• How much to wager when you have edge? (Hint: median not mean outcomes!) by Moontower

• Bet Sizing Is Not Intuitive by Moontower

• Fortune’s Formula on The Kelly Criterion by Moontower
 

Moontower Notes

Formulas

Noteworthy Observations & Quotes

• Two keys are needed to unlock success in professional gambling, trading and investing:
1. Profitable opportunities
2. Sizing investments/bets (correctly)

• A trader with a mediocre strategy and a great risk model will become fairly successful. A trader with a great strategy and a mediocre risk model will become bankrupt.

• The Kelly Criterion only defines the 'Optimal' bet to maximize return.  It does not use caution or assign value to risk. It is limit not a goal!

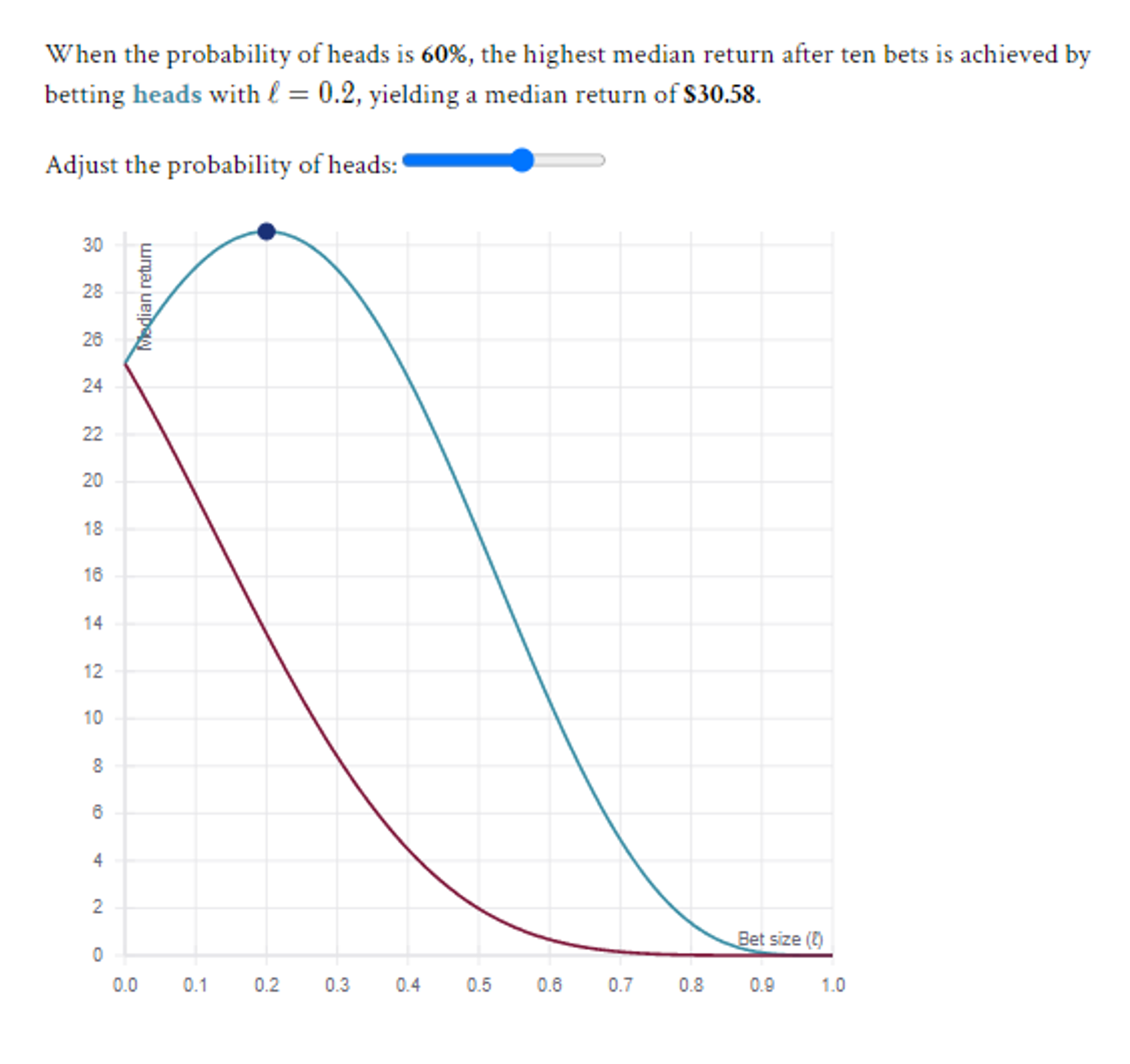
• Ask what maximizes wealth for the median outcome. That will also be the solution to optimal Kelly fraction.