- Skew is also positively correlated to term structure
- BANKRUPTCY LIFTS BOTH SKEW AND TERM STRUCTURE
- IMPLIED VOL IS ‘STICKY’ FOR LOW STRIKES AND LONG MATURITIES Term structure should rise if near-dated ATM implieds fall, as far-dated ATM implieds are relatively constant (as they tend to include complete economic cycles)
- Teeny puts are sticky If there is a sudden decline in equity markets, it is reasonable to assume realised volatility will jump to a level in line with the peak of realised volatility. Therefore, low-strike, near-dated implieds should be relatively constant (as they should trade near the all-time highs of realised volatility). If a low-strike implied is constant, the difference between a low-strike implied and ATM implied increases as ATM implieds falls. This means near-dated skew should rise if near-dated ATM implieds decline.
(this relationship can break down in panicked markets)
The correlation between skew and term structure is shown below. The diagram only shows
data for positive term structure, as the relationship tends to break down during a crisis.
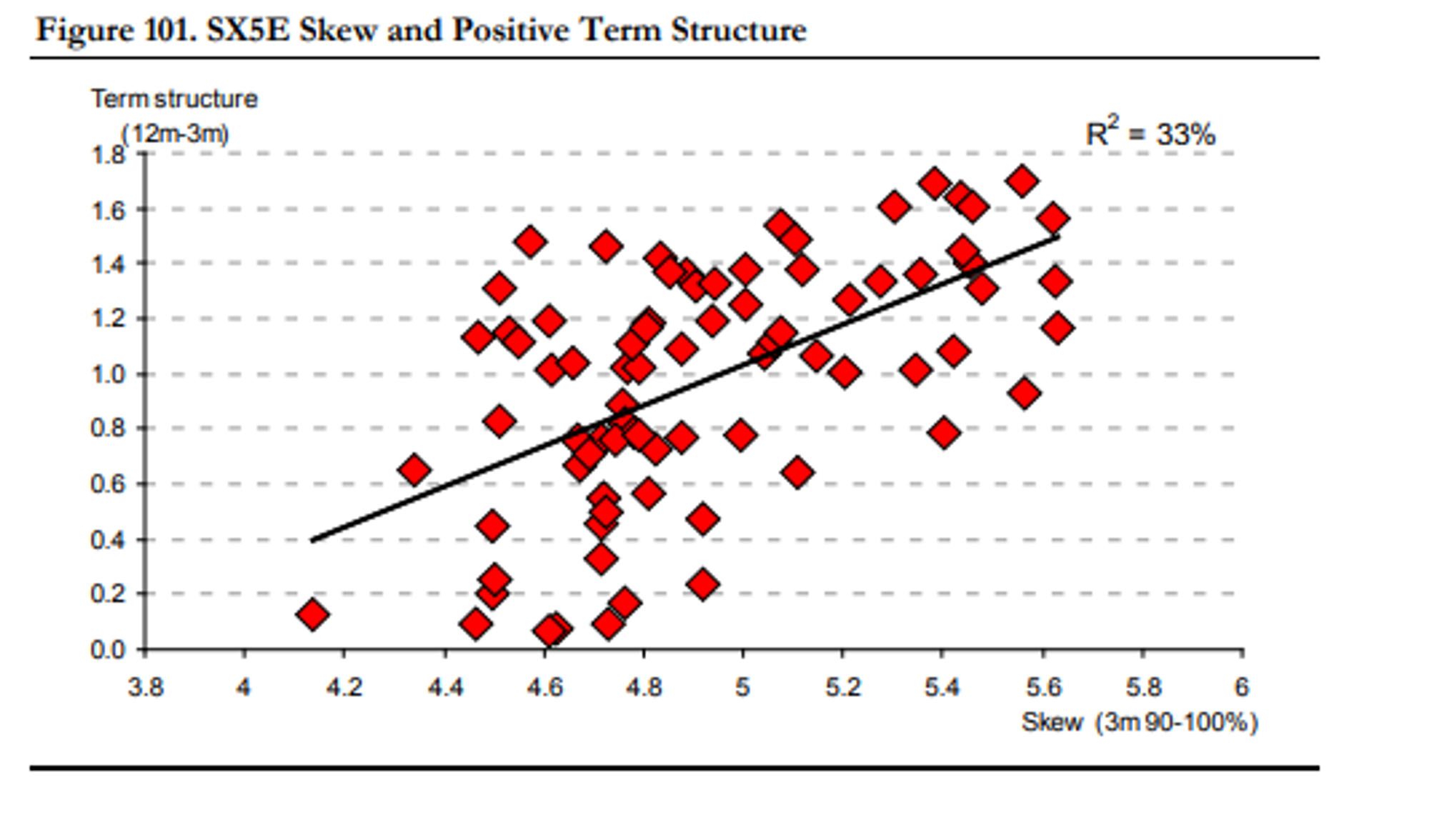
Theories for this correlation:
There are various models that show the effect of bankruptcy (or credit risk) lifting both skew
and term structure. As implieds with lower strikes have a greater sensitivity to credit risk (as most of the value of low strike puts is due to the risk of bankruptcy), their implieds rise more, which causes higher skew. Similarly, options with longer maturity are more sensitive to credit risk (causing higher term structure, as far-dated implieds rise more). Longer-dated options have a higher sensitivity to credit risk as the probability of entering default increases with time (hence a greater proportion of an option’s value will be associated with credit events as maturity increases).
Therefore term structure & skew are correlated as both rise as implied volatility falls
- Term structure shifts
In practice, term structure tends to shift in root (T) manner (me: aka constant straddle spreads) but occasionally parallel shift.
As implieds rise, skews flatten and vice versa
If implieds rise (or decline) in a square root of time manner when equities decline (or rise), then this causes skew to decay by the square root of time as well (assuming sticky strike) [because nearer dated skew is steeper
So the skew as measured by vertical spreads implies a scaling factor for the term structure and vice versa